The Law of Large Numbers
The law of large numbers (LLM) is one of the most fundamental theorems of statistics. It states that the average value of a repeatedly performed random experiment tends to the mean value. But what does this mean? And why is it so powerful?
Let \(x\) be a random variable with distribution \(p(x)\), and let \(x_1, \dots, x_n\) be \(n\) random draws from \(p(x)\). Denote the mean of \(x\) by \(\mu : = \mathbb{E}[x]\) and define the mean statistic for a sample of size \(n\) as \(\bar{x}_n : = \frac{1}{n}\sum_{i=1}^n x_i\).
Then, the law of large numbers states that
\[\bar{x}_n\xrightarrow[n \to \infty]{} \mu\]that is for a large enough sample size \(n\), the mean statistic tends towards the population mean.
This is a remarkable statement since, simply by random sampling, one can estimate the average value of a whole polulation. For instance, it might be infeasible to compute \(\mu\) directly if the population is very large but we can compute the average of a much smaller random sample instead.
The question arises now, how large \(n\) needs to be to get a somewhat reliable estimate? For now we’ll give an empirical answer for the special case of coin tosses. The concept of coin tosses is more general than the name suggests, as the same technique is applied when computing counts or percentages e.g., when asking which percentage \(\mu\) of all voters support the current government. In those cases “heads” would mean that a random voter supports the government, and “tails” would mean that they do not. But for the sake of this blog post we’ll stick with the analogy of coin tosses.
Tossing a coin \(n\) times
We’ll consider the case of a fair coin \(\mu=0.5\) and produce Bernoulli random samples \(x_1, \dots, x_n \in \{0, 1\}\). This means, “heads” will come up with probability \(\mu\) and “tails” with probability \(1-\mu\). We’ll assign the value “1” to “heads”, and “0” to “tails”.
In practice, we would only have access to the sample \(x_1, \dots, x_n\), and the statistic \(\bar{x}_n\) would be used to estimate the unknown parameter \(\mu\). But in this blog post we want to illustrate how fast \(\bar{x}_n\) gets close to \(\mu\), hence we simulated the sample from the distribution with parameter \(\mu\) and then check how well our estimator does. We first draw the sample:
import numpy as np
np.random.seed(42)
# fair coin
mu = 0.5
# Bernoulli samples: 1 means heads, 0 means tails
n_samples = int(1e5)
samples = 1 * (np.random.rand(n_samples) < mu)
# print the first 10 samples
print(samples[:10])
array([1, 0, 0, 0, 1, 1, 1, 0, 0, 0])
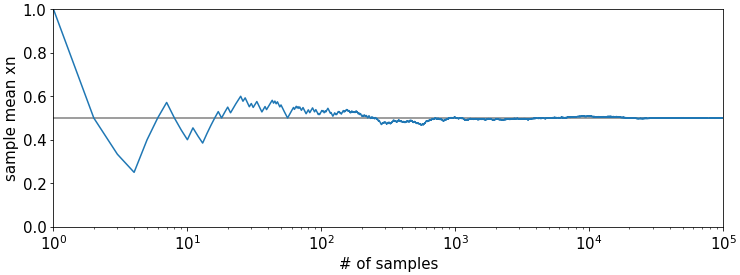
We now compute the mean statistic \(\bar{x}_n\) for an increasing sample size \(n=1,\dots,1e^5\).
S = np.cumsum(samples)
n = np.arange(1, n_samples + 1)
means = S / n
We plot \(\bar{x}_n\) over \(n\) in blue, and the true parameter \(\mu\) in gray as horizontal line. The x-axis is in log-scale. We see that \(\bar{x}_n\) gets quite close to \(\mu\) for \(n\) larger than roughly 100. This is an astonishingly small number considering that we could estimate real parameters such as voter percentages with the same technique. Of course the real world is a bit more tricky, but the general observation holds that sample sizes \(n\) often need not be overly large such that statistics \(\bar{x}_n\) somewhat accurately represent parameters of quite large populations.
The strong and weak LLN
We did not specify above what the statement \(\bar{x}_n\xrightarrow[n \to \infty]{} \mu\) means precisely. It’s also not super straightforward to define since the sequence \(\bar{x}_n\) is not deterministic (remember, we’re tossing coins and averaging the outcome). In fact, there are typically two definitions.
The first one is the weak law of large numbers (weak LLN) which implies convergence in probability, that is \(\lim_{n\rightarrow \infty}P(|\bar{x}_n - \mu| > \epsilon)=0\) for all \(\epsilon > 0\). In words this means that for any \(\epsilon, \delta > 0\) there exists an \(n\) (that depends on \(\delta\) and \(\epsilon\)) such that \(\bar{x}_n\) will be inside a ball of radius \(\epsilon\) centered at \(\mu\) with probability \(1-\delta\). That means that any random sequence will eventually have a high probability to be close to \(\mu\); although for finite \(n\) we can never quite box all \(\bar{x}_n\) inside the ball, only with high probability \(1-\delta\).
The second one is the strong law of large numbers (strong LLN) which implies that \(\bar{x}_n\) converges to \(\mu\) almost surely that is \(P(\lim_{n\rightarrow \infty} \bar{x}_n = \mu) = 1\). It means that the probability of the event for which the sequence \(\bar{x}_n\) does not converge to \(\mu\) in the classic sense is zero. This is a stronger statement as it implies that there exists an \(n\) for which the probability for all \(\bar{x}_{m>n}\) to be outside a ball of radius \(\epsilon\) is zero, i.e, we can box in all \(\bar{x}_n\) with probability 1 at some point. Any strongly convergent sequence is also weakly convergent.
In practice, both of the above statements mean that for large enough \(n\), the sample mean \(\bar{x}_n\) can represent the population mean \(\mu\) quite well as we have seen in the plot. In terms of tossing a fair coin, and somewhat pictorially, convergence means that the event of any sequence of “heads” and “tails” that does not average to half “heads” and half “tails” in the long run, such as e.g., only “heads” \([1, 1, 1, 1, \dots]\) has vanishing probability.
What is the catch?
There is always a catch of course. And in the case of LLN it is probably that it requires us to draw truly random numbers from \(p(x)\). In the example above it was easy to do as Numpy provides us with a pseudo-random number generator. However, if \(p(x)\) relates to the real world, and is less accessible, producing a random sample is often not easy at all. In this case the sample can have several unknown biases, e.g., selection bias, and the statement \(\bar{x}_n\xrightarrow[n \to \infty]{} \mu\) does not hold anymore. But this is a topic for another blog post :)